ABSTRACT

学习复杂的网络动力学是理解、模拟和控制现实世界复杂系统的基础。尽管人们在预测网络节点的未来状态方面做出了巨大努力，但捕捉长期动态的能力在很大程度上仍然有限。这是因为他们忽略了一个事实，即复杂网络的长期动态主要受其固有的低维流形（即骨架）支配。因此，我们提出了动态不变骨架神经网络（DiskNet），它基于双曲空间的重整化群结构来识别复杂网络的骨架，从而同时保留拓扑和动力学特性。具体来说，我们首先通过物理信息双曲嵌入将具有各种动力学特性的复杂网络浓缩为简单骨架。然后，我们设计图神经常微分方程来捕捉骨架上的浓缩动力学。最后，我们使用基于度的超分辨率模块将骨架网络和动力学恢复为原始网络和动力学。通过对三个代表性动态以及五个真实世界和两个合成网络的广泛实验，证明了所提出的 DiskNet 的卓越性能，就长期预测准确率而言，它比最先进的基线平均高出 10.18%。转载代码请访问：https://github.com/tsinghua-fib-lab/DiskNet

1 INTRODUCTION

现实世界中许多复杂系统的演化行为，如大脑[9]、社会网络[51]和生态系统[15]，都可以建模为复杂网络的动力学[4]，其中系统内的组件被视为网络中的节点，组件之间的耦合相互作用被视为边[13]。学习这些复杂网络的动力学有助于提高分析这些网络的能力，从而促进众多重要应用，包括了解其内在弹性[13]、预测其未来状态[31, 35]和控制其状态[28]等。然而，复杂网络中通常存在大量节点和边。一方面，大规模网络大大增加了复杂网络推理和估计任务的计算复杂度。另一方面，大量不太重要的节点作为干扰变量，有可能阻碍我们揭示网络的有效动态[13]。在这种情况下，一个基本问题出现了：给定一个任意的复杂网络，我们能否找到一个低维骨架，在此骨架上对粗尺度的长期动态进行建模，从而获得较高的预测性能和较低的计算成本？

作为一个长期存在的问题，人们开发了许多方法来降低大规模网络的维度，包括统计物理方法[41]和机器学习方法[20, 22]。其中，统计物理方法利用重整化群技术[14, 40]来识别保留度分布和聚类系数的骨架。机器学习方法 [20, 22] 学习图粗化策略，以保持原始网络与使用粗化网络重建的网络之间的拓扑和节点特征一致性。所有这些方法都只保留了静态拓扑和节点信息，忽略了网络的动态变化 [14、20、22、40]。因此，它们无法捕捉节点动态的集体行为，无法准确预测其长期演变。此外，有几种分析方法表明，复杂网络动态的关键属性，如弹性 [13] 或临界时间延迟 [29]，可以嵌入到一个超低维度的子曲面中 [13, 29]。然而，这些方法依赖于过于简化的网络拓扑假设，如均质节点度或基于度的均场[29, 39]，无法得到理想维度的骨架。综上所述，复杂的网络及其错综复杂的动态能否浓缩成低维骨架仍是一个悬而未决的问题。

然而，开发一种有效的方法来学习骨架和骨架网络上的相应动力学也是一项艰巨的任务，其中存在以下挑战。首先，确定有利于最准确预测复杂网络演化行为的骨架具有挑战性。骨架可以通过将节点集群粗分为超级节点来获得。然而，我们对如何在保留骨架网络内在动态的同时找到这样的簇缺乏足够的了解。其次，如何在骨架网络中的节点状态与原始网络之间建立可逆映射是第二个挑战。这涉及建立一个聚合函数，根据子节点计算超级节点的状态，以及一个提升函数，将每个超级节点的状态映射回子节点。由于聚合过程不可避免地会带来信息损失，因此如何建立一个高效的提升函数是一个关键问题

在本文中，我们提出了一种名为 “动态不变骨架神经网络（DiskNet）”的新型深度学习框架，用于识别双曲空间中复杂网络的低维骨架，为其长期动态建模。该框架通过物理信息嵌入来识别骨架。这些嵌入基于在双曲空间中开发的重整化群技术进行初始化，然后在端到端训练过程中进行微调，使知识与数据相结合，从而克服第一个挑战。然后，DiskNet 利用图神经常微分方程对骨架网络上的凝聚动力学进行有效建模。最后，它利用精心设计的基于度的超分辨率模块作为提升函数，将凝聚动态映射回原始网络。该模块利用节点在度数上的同质性来识别共享相同提升网络的节点群，从而构建有效的提升函数来解决第二个挑战。

contribution

我们建议根据重整化群理论中物理知识启发下的双曲嵌入来识别骨架，从而使我们能够结合知识和数据来学习有效的骨架。
我们开发了一个功能强大的图神经常微分方程（ODEs），并集成了一个新颖的超分辨率模块，利用度数接近的节点的同质性，使我们能够精确地模拟骨架上的凝聚动力学，并将其映射到原始网络中。
在五个真实网络拓扑和两个合成网络拓扑的三个代表性网络动态上进行的大量实验结果表明，DiskNet 的预测准确率平均比最先进的基线高出 10.18%，这表明了它的优越性。

2 PROBLEM FORMULATION

在不失一般性的前提下，网络拓扑由邻接矩阵 $A \in {0, 1}^{N \times N}$ 表示，其中每个元素 $a_{ij}= 1$ 表示节点 i 和 j 之间的连接。网络动力学描述了图 G 上节点状态的演化，其中考虑了每个节点的自动力学以及与其邻居的交互作用，其方程为

$\frac{dx_i}{dt} = f(x_i) + \sum^{N}_{j \neq i}{a_{ij}g(x_i,x_j)}$

其中，f 表示自动力学，g 表示节点间的耦合动力学。节点状态矩阵表示为 $\textbf{X} \in \mathbb{R}^{N \times L \times d}$ ，代表在连续的 L 个时间步序列中 N 个节点的 d 维状态的观测值。

此外，我们认为图 G 的骨架为 $Gs = (\mathcal{V}_s, A_s)$，其中 $A_s \in {0, 1}^{\gamma N \times \gamma N}$ 描述了集合 $\mathbb{V}_s$ 中超级节点（定义为原始节点的聚合）之间的连接。这里，γ 表示骨架相对于原始拓扑的缩减率、given by $γ = \frac{V_s}{V}$ .超级节点与原始节点之间的对应关系由赋值矩阵 $P \in {0, 1}^{\gamma N \times N}$ 定义，其中 $p{ij} = 1$ 表示节点 j 被聚合为超级节点 i。函数 $x{s,i}=u(x{Pi})$ 描述了超级节点 i 的状态如何从其子节点汇总而来。骨架上网络的动态定义与公式 1 相同，表示为 $\frac{dx{s,i}}{dt}$。超级节点的状态通过提升函数 v 映射回其子节点，即 $xi = v(x{s,i})$ 。我们强调，通过聚合而非剪枝获得网络骨架的目的是将相似节点的集体动态整合为一个具有代表性的超级节点。

我们的目标是确定赋值矩阵 P、状态聚合函数 u 和提升函数 v，从而建立图 G 的低维骨架 $Gs$ 。随后，通过在骨架上建立动态模型 $\frac{dx{s,i}}{dt}$ 并将其映射回子节点，我们的目标是在给定历史观测值 $X{lookback}$ 的情况下，实现对节点状态长期演化 $X{horizon}$ 的准确预测。整个过程如图 1 所示

3 METHOD

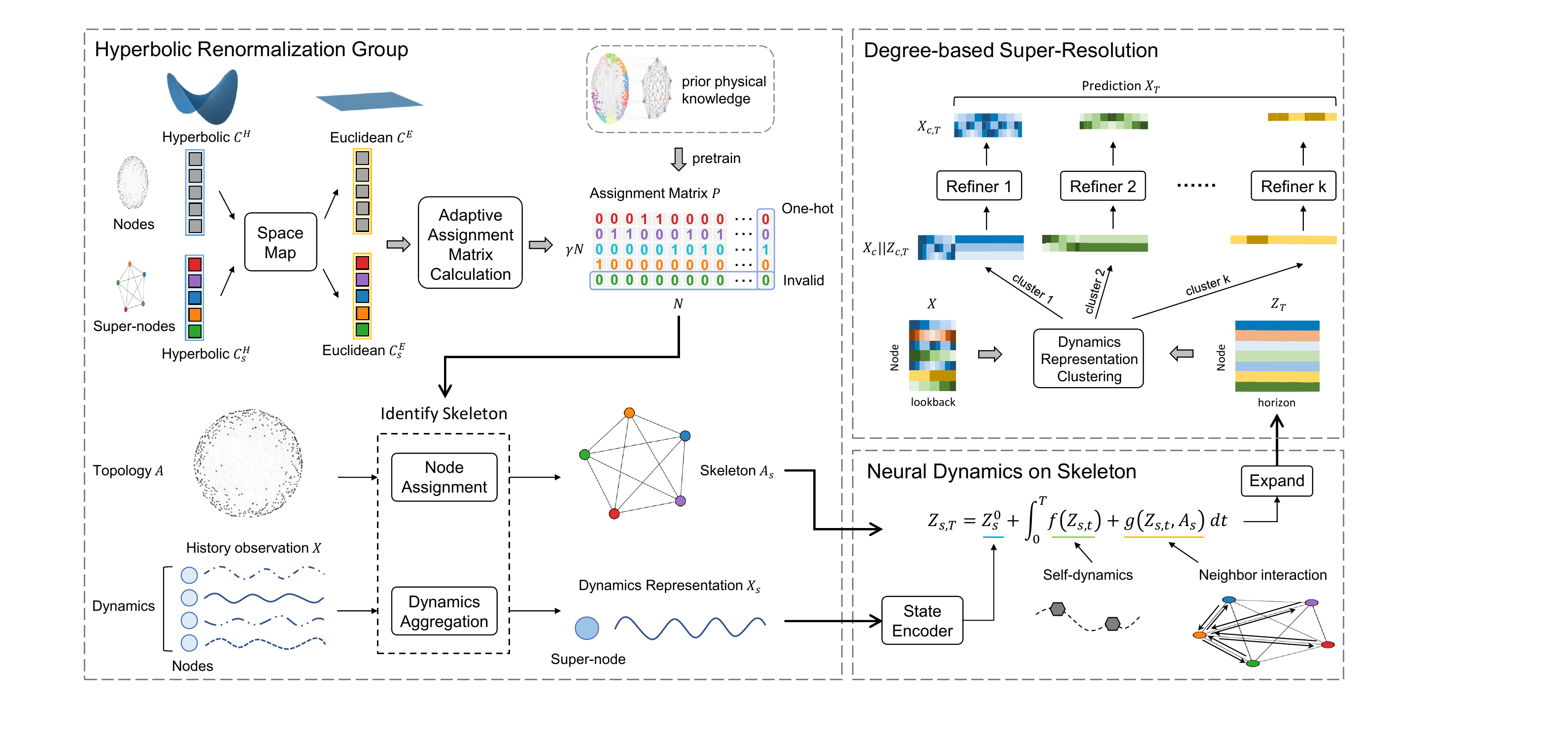
在本节中，我们将提出动态不变骨架神经网络（DiskNet），通过识别双曲空间中的骨架来预测复杂网络的长期动态。整体框架如图 2 所示。根据上述挑战，我们首先提出了双曲重整化群（RG）模块，利用双曲几何的强大表示能力捕捉节点的拓扑和动态相似性，并自适应计算赋值矩阵，指导节点赋值和动态聚合。然后，设计了一个神经 ODE 模型来模拟骨架上超级节点的神经动力学，其中包含两种机制：自我动力学和邻居相互作用。最后，提出了一个基于度聚类的超分辨率模块，将骨架上的动态表示提升到原始节点上。

3.1 Hyperbolic Renormalization Group

给定复杂网络的邻接矩阵 A，识别网络骨架 $A_s$ 的关键在于根据网络的拓扑特性和节点动态的潜在相似性确定赋值矩阵 P。我们在双曲空间 [26] 中测量原始节点和超级节点之间的相似性。在此基础上，我们推导出一个自适应分配矩阵，为每个超级节点聚合子节点的动态表示，该矩阵共同包含拓扑和动态特征。我们通过初始化超级节点的双曲嵌入来引入先验物理知识，从而指导模型训练。

3.1.1 learnable hyperbolic embedding 庞加莱盘是一种二维双曲几何，负曲率特性使节点嵌入之间的双曲距离与它们在图中的距离相一致。相同维度的双曲空间比欧几里得空间容量更大，因此更适合表示大规模网络中节点的拓扑和动态信息。庞加莱盘上两点之间的距离为

$d^c_H(x,y)=\frac{1}{\sqrt{|c|}}\mathrm{arcosh}(1-\frac{2c||x-y||^2}{(1+c||x||^2)(1+c||y||^2)})$

以前的工作主要是学习网络拓扑的双曲嵌入 $C^H \in R^{N \times 2}$ ，初始化后将其冻结在 DiskNet 中，用于对原始拓扑进行分层表示。我们的核心理念是为每个超级节点维护一个可学习的双曲嵌入 $C^H_s \in R^{\gamma N \times 2}$ ，以捕捉其所有子节点的动态特征.我们首先根据第 4.3.4 节所述方法初始化 $C_s^H$ ，引入先验物理知识，然后在端到端训练过程中对其进行微调。考虑到在欧几里得空间定义的计算规则不适用于双曲空间的矢量，我们使用对数映射将 $C^H$ 和 $C^H_s$ 投影到相应的欧几里得坐标上。

$\theta^E_z=\frac{2}{\sqrt{|c|}\lambda^c_z}\mathrm{arctanh}(\sqrt{|c|} ||-z \oplus_c \theta^H||)\frac{-z \oplus_c \theta^H}{||-z \oplus_c \theta^H||}$

其中，$\oplus_c$ 表示莫比乌斯加法 [30]， $\lambda^c_x=\frac{2}{1+c||x||^2}$ 。 $\theta^H$ and $\theta^E$ 分别表示双曲空间和欧几里得空间中的向量。与大多数研究[26, 32, 34, 42]一致，双曲流形的切线空间选在原点 $\mathbb{O}$，曲率设为-1。我们将在第 4.3.2 节中详细验证双曲嵌入在表示节点拓扑和动态相似性方面的优越性。

3.1.2 Adaptive assignment matrix. 根据原始节点和超级节点的双曲嵌入，我们计算出自适应赋值矩阵为

$P = {\rm softmax}(\tilde{C}_s\tilde{C}^T)$

其中，softmax 按行计算，$\tilde{C} = MLP(C^E)$ 和 $\tilde{C}s = MLP(C^E_s)$。我们最小化$L_E=\frac{1}{N}\sum^N{i=1}{H(P_i)}$，其中 H 表示熵函数，$P_i$ 是 P 的第 i 列，以限制赋值矩阵的每一列都接近单热向量。此外，我们最小化 $L_R=||A,P^TP||_F$ 来启发式地引导赋值矩阵保持原始拓扑的骨架，其中 $||\cdot||_F$ 表示弗罗贝尼斯规范。

3.1.3 Node dynamics aggregation. 我们采用图卷积神经网络来捕捉原始节点的动态传播，并将其聚合为超级节点的动态表示，即

$H = \sigma((\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} X) \Theta_1) \in \mathbb{R}^{N \times d},$ $X_s = PH \in \mathbb{R}^{\gamma N \times d}$

其中，$\tilde{D} = \sum{j}{\tilde{A}{ij}}$，$\tilde{A} = A + I$,$\Theta$ 为可学习参数。超级节点之间的连接由邻接矩阵 $As = PAP^T$ 描述，其中元素 $a{s,ij}$ 表示超级节点内部（i = j）或不同超级节点之间（i≠ j）的子节点连接总数。

3.1.4 Physics-informed initialization. 统计物理学将节点相似度的意义赋予节点嵌入波恩卡莱盘的角坐标，并采用基于角坐标的重整化群[14]。这种设计有助于保留骨架中网络拓扑的度分布和聚类系数。虽然这种方法不能保证有效地表示网络动态，但 DiskNet 可以在随后的端到端训练中自动调整超节点的可学习双曲嵌入。因此，我们根据角坐标对原始节点进行排序，并将其划分为 $\frac{1}{\gamma}$ 个节点的节点组，以预先定义赋值矩阵 $P0$ ，用于预训练自适应赋值模块，其损失函数为 $L_p = \frac{1}{\gamma N^2}\sum{|P-P_0|}$。我们在附录 C 中提供了预训练阶段的伪代码。超级节点的双曲嵌入初始值设为 $c^H{s,i} = \frac{1}{|P{0,i}|}\sum{j \in P{0,i}}{c^H_j}$，其中 $P{0,i}$ 表示属于超级节点 i 的子节点集。

3.2 Neural Dynamics on Skeleton

在获得网络动力学骨架和超级节点的聚合状态后，我们将网络动力学形式保持为公式 1，并使用神经 ODE 对其进行建模

3.2.1 ODE function

现在我们定义骨架潜在动力学 $\frac{dZs}{dt}$ 的前向 ODE 函数。考虑到每个超级节点 $x{s,i}$ 的演化受其自身动力学和耦合动力学的影响，参数化的时间导数由两部分组成：一部分是自动力学函数 $f(Z_s)$ ，另一部分代表与邻近节点的相互作用 $g(Z_s, A_s)$。因此，每个超级节点的动态方程为

$\frac{dZ_s}{dt} = f(Z_s) + g(Z_s, A_s)$

其中，f 是 MLP，g 是负责信息传播的 GNN

$g(Z_s, A_s) = \sigma(A\sigma(Z_s\Theta_3)\Theta_2) .$

3.2.2 Solve 给定 ODE 函数后，骨架动力学的预测轨迹可由任何 ODE 求解器作为初值问题求解

$Z_{s,T} = Z_{s,0} + \int^T_0{f(Z_{s,t}) + g(Z_{s,t}, A_s) dt}$

其中，初始状态 $Z_{s,0} = MLP(X_s) \in \mathbb{R}^{\gamma N \times 1}$。这样，我们就可以预测超级节点在任意连续时间点 T 的状态。

3.3 Lift to Original Nodes

在获得骨架上超级节点的预测轨迹后，需要将其提升回原图中的每个独立节点，以完成网络动态预测。然而，在超级节点的聚合过程中，不可避免地会出现信息丢失，例如同一超级节点内子节点状态的异质性。简单地将超级节点的预测值复制到其子节点上并不足以实现准确的扩展。为了克服这一难题，受统计物理学研究的启发 [13, 29]，我们设计了一个基于度聚类的超级分辨率模块。

3.3.1 Degree-based clustering. 通过采用程度加权平均场方法，可以将程度相似节点的状态和临界点压缩到一个超级节点中进行预测 [13, 27, 29] 。这意味着节点的集体动态表现出了与节点度数有关的同质性。受此启发，考虑到现实世界的网络通常遵循幂律分布，我们选择使用度数对数作为特征，通过 K-means 算法对节点进行聚类，并在每个聚类中执行超分辨率。事实上，在 Poincaré 磁盘中，节点的度数直接对应于其径向坐标。因此，具有相似径向坐标的节点应被识别为属于同一个超级节点。

3.3.2 Super-resolution. 基于骨架动态的有效表示，超分辨率模块的设计不需要太复杂。我们用 $Nc$ 表示第 c 个集群中的节点集，用 Xc 表示它们的历史观测值，用 $Z{c,T}$ 表示相应超级节点的预测值。由于扩展操作只是简单地将超级节点的预测值复制到其子节点，而不进行区分，因此 Zc,T 是对每个节点的粗略和同质预测。我们根据历史观测值 $Xc$ 对 $Z{c,T}$ 进行细化，得到精确预测值为

$X_{c,T} = \sigma((h_0 || h_1)\Theta_4)$

其中 || 表示连接操作， $h0 = MLP(X_c)$ and $h_1 = MLP(Z{c,T})$ 。这样，我们就完成了网络动态预测。我们将在第 4.4.2 节中证明，随着集群数 k 的增加，预测精度将迅速达到上限。因此，有限的 k 设置足以实现良好的预测性能。

3.4 Training

现在我们介绍 DiskNet 的训练过程。在开始端到端训练之前，我们首先初始化原始节点和超级节点的双曲嵌入（如第 4.3.4 节所述），并利用先前的物理知识预训练自适应赋值模块。随后，在每次迭代中，模型都会在损失函数 LE 和 LR 的指导下学习自适应分配矩阵。骨架动态预测使用 L2 误差进行更新，即 $Ls = MSE(\overline{Z}{s,T}, Z{s,T})$ ，其中 $\overline{Z}{s,T}$ 代表超级节点的预测状态，$Z_{s,T}$ 是根据赋值矩阵和状态编码器获得的基本真实值。最后，利用所有原始节点预测的 L2 误差 $L_p = MSE(\overline{X}_T, X_T)$ 更新超分辨率模块。由于 Poincaré 盘是欧几里得空间的保角映射，因此在用梯度更新节点嵌入时，必须根据黎曼度量张量来缩放梯度。

$\nabla_H(\theta) = (\frac{1-||\theta||}{2})^2 \nabla_E(\theta)$

其中，$\nabla_E(\theta)$ 和 $\nabla_H(\theta)$ 分别是向量 θ 的欧氏梯度和双曲梯度。完成端到端训练后，我们分别对超分辨率模块进行微调，以提高预测性能。

4 EXPERIMENTS

在本节中，我们将介绍 DiskNet 的评估结果。我们首先介绍了用于测试的动态和网络拓扑结构，然后介绍了用于比较的基线。然后，我们分析了长期预测性能、识别骨架的可解释性以及敏感性分析。附录 B 提供了所有实验的软件和硬件环境的详细信息。

4.1 Experiment Setup

我们对三个具有代表性的非线性动态系统进行了实验，在五个真实世界的网络拓扑结构和两个合成拓扑结构上运行。有关数据集生成的详细信息，请参见附录 A.2。

4.1.1 Network Topology. 我们考虑了基础设施、社交网络、大脑网络和万维网 1 中的五个真实世界网络拓扑结构[36]：(a) 美国的电网（PowerGrid）；(b) 果蝇的大脑网络；(c) 互赞的 Facebook 页面（Social）；(d) 链接到 www.epa.gov 的页面（Web）；(e) 两个非美国机场之间的联系（Airport）。此外，我们还考虑了两个合成网络：(f) Barabási-Albert 网络 (BA) [3]；(g) Watts-Strogatz 网络 (WS) [43]。所有拓扑结构的统计特征如表 1 所示。

4.1.2 Network Dynamics. 我们考虑了生物学和物理学中三种有代表性的动力学：(a) Hindmarsh-Rose 动力学[6]，(b) FitzHugh-Nagumo 动力学[12]，(c) Coupled Rössler 动力学[1]。相关方程和参数设置详见附录 A.1

4.2 Baseline

在所有数据集上，我们与以下基于 GNN 的最先进方法进行了比较

DCRNN [24] 采用双向随机行走和编码器-解码器架构，通过计划采样实现准确的时空预测。
GraphWaveNet [44] 采用自适应依赖矩阵，通过节点嵌入捕捉隐藏的空间依赖关系。
AGCRN [2]：引入了两个自适应模块和递归网络，可自动捕捉交通序列中细粒度的空间和时间相关性。
NDCN [50] 通过结合神经 ODE 和 GNN，捕捉复杂网络上的连续时间动态。
STGNCDE [10] 将时空图神经网络与神经控制微分方程相结合，用于预测多变量时间序列。
MTGODE [19] 将多变量时间序列抽象为具有随时间变化的节点特征的动态图，并对其在潜空间中的连续动态进行建模。
FourierGNN [48] 是最先进的多变量时间序列预测 GNN 模型。它引入了超变量图，并在傅立叶空间中执行矩阵乘法。

4.3 Performance Evaluation

在本节中，我们将分析 DiskNet 的长期预测性能、识别骨架和计算成本。

4.3.1 Long-term Prediction. 我们根据平均绝对误差 (MAE) 评估了 DiskNet 对所有拓扑结构和动态的长期预测性能。我们为模型提供了过去 12 个时间步的观测轨迹，并要求其预测未来 120 个时间步的节点状态。在所有实验中，DiskNet 的缩减率 γ 和集群数 k 分别设置为 50%和 10，设置的原因将在第 4.4 节中解释。

120 个时间步的平均性能如表 1 所示。值得注意的是，在几乎所有情况下，DiskNet 的长期预测性能都远远优于所有基线，在某些情况下提高幅度超过 50%。此外，我们还可以观察到，即使是最先进的模型，次优模型在不同场景下也会有所不同，这表明它们的性能存在波动。这一方面表明，我们的方法能够在各种情况下准确识别网络动力学骨架并建立模型。另一方面，它也强调了低维骨架对于稳定、准确的长期预测的重要性。相比之下，同样采用图神经 ODE 的 NCDN 和 MTGODE 模型只在少数情况下表现良好，这可能是因为它们对整个网络进行建模时，没有有效地聚合节点的关键集体行为。

4.3.2 Dynamics Skeleton. 然后，我们通过对比实验和可视化分析来研究 DiskNet 所识别的动态骨架。我们比较了启发式、图池和重整化组等五种基线方法：(a) 随机分配；(b) 基于节点度的阈值分配；(c) 基于中心度的阈值分配；(d) DiffPool [49]；(e) GMPool [21]；(f) 静态 RG [14]。前三种方法都是根据一定的规则选择超级节点，然后将子节点随机分配给超级节点。两种图池方法的赋值规则与原论文一致。RG 方法仅根据节点的拓扑特征分配节点，因此被称为静态 RG。在所有实验中，为确保公平性，在使用基线获得分配矩阵后，使用 DiskNet 对状态聚合和骨架动力学等模块进行端到端训练。所有模型的缩减率 γ 设为 50%。

如表 2 所示，我们在所有拓扑结构中对 Hindmarsh-Rose 动力学进行了实验。凭借双曲空间强大的表示能力，DiskNet 确定的骨架捕捉到了节点的长期动态变化，从而在所有场景下都能获得比基线更准确的预测结果。启发式方法只考虑拓扑特征而忽略了节点动态，在某些情况下表现不如随机分配法。此外，用欧几里得空间表示节点动态以推导赋值矩阵的图集合方法无法像双曲空间那样有效地测量节点相似性和捕捉潜在的动态交互。在节点分类任务中也有类似的观察结果 [32，33]。虽然静态 RG 方法也利用双曲几何来表示节点特征，但它在计算赋值矩阵时只考虑了静态拓扑特征，而忽略了节点动态的相似性。因此，它无法识别长期动态的骨架.

我们在图 4 中展示了静态 RG 方法和 DiskNet 在相同拓扑但不同动态条件下识别出的骨架，其中动态曲线代表所有节点的平均轨迹。我们使用了缩减率 γ = 0.02% 的 500 节点 BA 网络的结果，以避免因网络规模过大而造成视觉混乱（表 1 中真实世界网络的可视化骨架见附录 D.1）。由于静态 RG 方法不考虑动态性，因此如图 4(a) 所示，三种动态下识别出的骨架是相同的。相比之下，DiskNet 在不同动力学条件下识别出的骨架存在差异。对于 FitzHugh-Nagumo 动力学（图 4(c)）和耦合罗斯勒动力学（图 4(d)），所有节点都表现出振荡行为，DiskNet 识别出的超级节点数量相似，分配模式也相似。然而，对于节点动态各异但趋势简单的 Hindmarsh-Rose 动力学，相应的骨架往往能捕捉到较少的超级节点。

对 DiskNet 所识别骨架的进一步分析表明，大多数超级节点与其子节点共享相同的局部邻域，但也存在子节点位置偏离的情况，尤其是在 Hindmarsh-Rose 动力学中（图 4(b)）。现有研究[14]已经证明，如果只考虑拓扑特征，在庞加莱圆盘上具有相似角度的节点应该属于同一个超级节点，而 DiskNet 则表明，如果考虑节点的动态特性，这一结论就不再成立。由于具有相似的动态特性，即使角度坐标有本质区别的节点也可能被分配到同一个超级节点中。此外，我们还观察到，具有相同角度坐标的节点可能会因为径向坐标的不同而被分配到不同的超级节点，这归因于节点度数与其动态之间的相关性[29]。最后，值得注意的是，有些超级节点只分配了少量的子节点，这将在第 4.4.1 节中进一步解释。

4.3.3 Computational Cost. 在推理过程中，DiskNet 只需要对骨架上的前向 ODE 函数进行积分，与之前基于神经 ODE 的方法相比，大大节省了计算资源。我们比较了在不同拓扑结构上使用不同缩减率 γ 的 DiskNet 和其他两种基于神经 ODE 的基线方法，以衡量单样本推理的时间成本。图 5 中的结果表明，即使有超分辨率模块带来的额外计算开销，γ = 50% 的 DiskNet 也能达到与 NDCN 相当的性能。事实上，随着网络规模的增大，网络动力学的降维潜力往往超过 50%（我们将在第 4.4.1 节中验证这一点）。因此，在预测大规模网络动态方面，DiskNet 比以往基于神经 ODE 的方法具有更高的实用价值。

4.3.4 Physics-informed Initialization. 表 1 中 DiskNet 的性能基于物理信息初始化，它允许模型从良好的初始点开始学习最佳参数.我们评估了耦合罗斯勒动力学上的 DiskNet 版本：(1) 没有初始化超节点的双曲嵌入和/或 (2) 没有预训练赋值矩阵计算模块。结果（如表 3 所示）表明，虽然在许多情况下，未进行物理初始化的 DiskNet 与基线版本相比具有竞争力，但始终不如物理初始化版本，这证明了物理初始化的必要性。

4.4 Sensitivity Analysis

在本节中，我们将分析两个重要超参数（即缩减率 γ 和聚类计数 k）对 DiskNet 预测性能的影响。

4.4.1 Reduction ratio. 缩减率 γ 设定了骨架中超级节点数量的上限。虽然模型会根据拓扑和动力学特性自动确定分配关系，允许一些超级节点不分配给任何子节点，但超级节点的比例不会超过 γ。我们在 BA 网络和 PowerGrid 网络中进行了耦合罗斯勒动力学测试，如图 6 所示。我们将占用率定义为在所有可用超级节点中至少分配到一个子节点的超级节点比例。观察发现，当 γ 小于 1%时，预测性能最差，占用率最高。这表明超节点的上限太低，无法确定合适的骨架。当 γ 超过 25% 时，预测性能变得相似。这既表明了网络动力学的低维特性，也表明将 γ 设为 50%一般就足够了，因为模型能够自适应地确定适当的占用率。最后，尽管两个网络都由大约 5000 个节点组成，但在相同 γ 条件下，PowerGrid 网络的占用率略高于 BA 网络。这表明，PowerGrid 电网中的耦合罗斯勒动力学具有相对较高的维度，给预测带来了更大的挑战，这与表 1 中的预测误差相对应。

4.4.2 Cluster count k. 集群数 k 代表超分辨率模块中细化器的数量，与预测性能呈正相关。不过，它需要与模型的参数大小保持平衡。我们对社交网络和 Web 网络中的 FitzHugh-Nagumo 动力学进行了不同时间尺度（horizon）的预测测试，如图 7 所示。当 k 小于 7 时，k 越大，预测误差越小。但是，当 k 超过 7 时，进一步增加 k 并不能显著提高性能。因此，我们建议在一般情况下使用默认的 10 k 值，这样可以在性能和计算成本之间取得平衡。

5.1 Learning Network Dynamics

现实世界中的许多系统都具有非线性和多尺度特性[23]，其动态常常被抽象为复杂的网络模型，从而说明节点之间的相互作用[5, 13, 25]。随着 GNN 等深度学习技术的发展，复杂网络动态的数据驱动建模受到了极大关注 [11]。Murphy 等人[31]提出了一种 GNN 架构，它能以最小的动力学假设精确模拟疾病在网络上的传播。NCDN [50] 结合了神经 ODE [8] 和 GNN，首次为复杂网络的连续时间动力学建模。Huang 等人[16, 17]分别通过引入边缘动力学 ODE 和环境编码器，成功地建立了动态拓扑和跨环境网络动力学模型。然而，尽管 [35, 38] 已经证明网络动力学是在一个非常低维的子空间中演化的，但现有的方法仍然是对整个拓扑结构的动力学演化进行建模，这就无法捕捉主导网络长期演化的低维结构。

5.2 Dimension Reduction of Complex Network

由于大规模网络的存储和计算成本较高，Serrano 等人[37]提出了差异过滤器，以确保在多尺度网络的剪枝过程中保留小尺度成分。García-Pérez等人[14]设计了基于角度相似性假设的双曲重整化群方法来识别复杂网络的低维骨架，Villegas等人[40]提出了一种基于拉普拉斯重整化群扩散的异构网络图像。Kumar 等人[22]以节点特征一致性为指导，通过端到端训练学习低维骨架。此外，一些关于图案学习的研究[18, 45]将原始图形中的每个图案视为超级节点，从而构建了一个聚集高阶几何特征的骨架。然而，这些方法只考虑了网络的静态特性，无法指导网络动态建模。Gao 等人[13]通过将原始系统映射到有效代表的一维系统来捕捉宏观动态，并进一步开发了基于度数的降维方法[29]，成功捕捉到了异构网络中相变的临界点。然而，这些基于专家知识的传统方法无法根据节点在不同拓扑结构和动力学条件下表现出的集体行为自动识别出最合适的骨架

5.3 Hyperbolic Graph Learning

双曲几何的负曲率特性导致了非线性距离度量，使其能够更好地捕捉图结构数据中的层次关系和非线性依赖关系。Nickel 等人[32, 33]将符号数据嵌入 Poincaré 球和洛伦兹模型，捕捉非结构化数据的层次结构和相似性。Liu 等人[26]和 Chami 等人[7]通过黎曼流形映射将双曲几何引入图表示学习，显著提高了节点分类任务的性能。Yang 等人[46, 47]进一步利用双曲几何对时变网络的层次结构进行建模。虽然这些工作证明了双曲几何适合表示网络结构数据，但在复杂网络动态建模方面仍缺乏应用。

6 CONCLUSIONS AND FUTURE WORK

本文通过一种基于双曲节点嵌入的骨架识别方法，探讨了复杂网络动力学的低维骨架及其在长期预测中的关键作用。通过在双曲空间中表示节点的集体动力学行为，我们计算了自适应赋值矩阵来识别骨架。然后，我们通过对超级节点的动态建模并将其提升到原始节点，从而实现有效的长期预测。广泛的实验结果表明，我们的模型在准确性和鲁棒性方面明显优于基线模型。此外，我们还验证了双曲几何在表示网络动态的低维结构方面优于欧几里得空间的能力。我们通过可视化结果，展示了同一拓扑结构上不同动态产生的不同骨架，从而证明了仅根据拓扑特征识别骨架的局限性。分析结果表明，在确保预测准确性的同时，不同类型的大规模网络的动态还具有丰富的降维潜力。未来，我们计划探索复杂网络的拓扑结构和动力学如何在确保预测准确性的同时影响可实现的最大降维。此外，我们还计划设计一种自动选择降维比率 γ 的机制。

Notes

RG(Renormalization Group)

通过缩放系统的不同部分，来简化系统的描述，并捕捉系统的整体行为。

尺度变换：在复杂系统中，我们可以将系统中的变量（如位置、动量、温度等）进行不同尺度的“重标定”或“缩放”。这种操作可以去除系统中无关的细节，保留重要的全局行为特征。
保持不变的物理量：通过这种缩放操作，系统的某些特征，如相变点、临界指数等，可以在不同的尺度上保持不变。这个“保持不变”的特性被称为“自相似性”或“重标定不变性”。
在复杂网络中的应用：在网络科学中，Renormalization Group 方法可以用来分析复杂网络在不同尺度下的结构特征，特别是在寻找网络的“骨架”（skeleton）或核心结构时。例如，论文提到的“degree distribution”（度分布）和“clustering coefficient”（聚类系数）等网络特性，可以通过RG方法被提取和保留，在不同尺度下仍然具有相似的统计性质。

复杂网络中的双曲几何

复杂网络连接一些可区分的异质的元素，这里的异质表明所有的节点可以以某种方式进行分类。一般情况下，这些分类表明，节点在分为一大组后还可以继续分为一些小的组。这些组和子组之间可以近似看为树结构，表示网络潜在的分层结构。而我们可以将树看作离散的双曲空间，双曲空间看作连续的树结构，从纯度量意义下，两者是相同的。
复杂网络的度幂律分布和聚类现象是双曲几何负曲率和度量性质的简单反映(例如，幂律度分布的指数是双曲空间曲率的函数)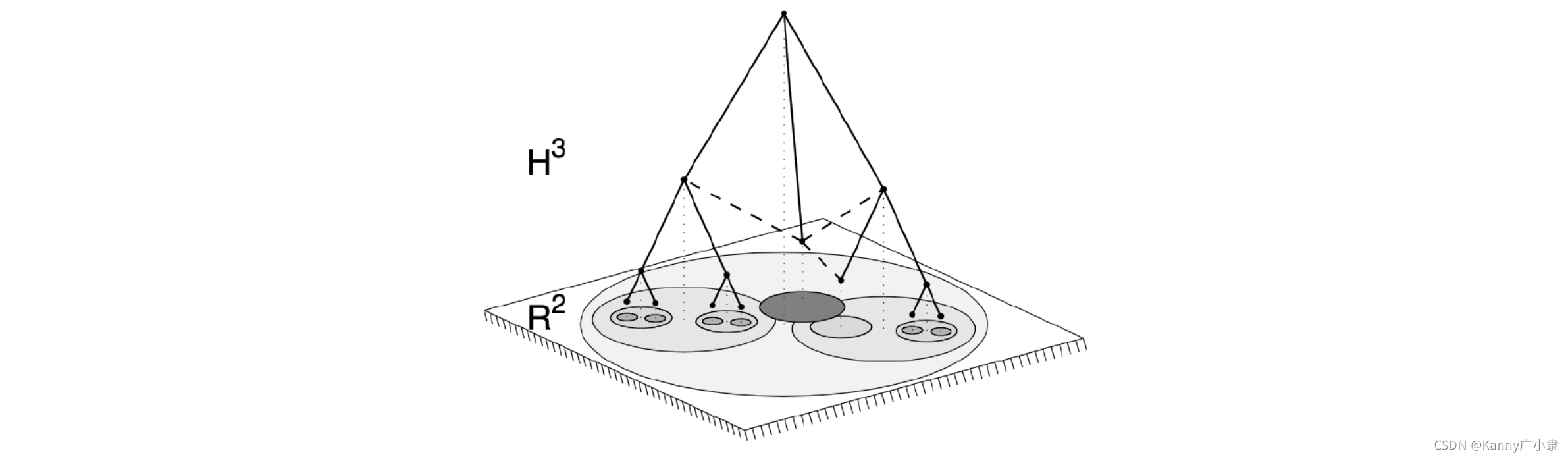；因此，如果假设节点属性首先具有某种度量结构，那么基于节点属性相似性的节点间距离可以映射到双曲空间中的距离。